ジェネラティブアートという言葉をご存知でしょうか？　アルゴリズムによって作られる芸術作品を指す名称です。Pinterestで「generative art」と検索すると静止画、動画ともにたくさんの作品を見ることができます。

無機質さを感じさせるものもあれば、まるで生きているように感じる作品もあります。創作者たちはどのようなところから着想を得ているのでしょうか？
彼らの中には数学的な幾何学模様や物理現象、果ては生物が織りなす複雑なパターンをコンピューターで再現することにより作品を作る者もいます。

本記事では特に「生物」に焦点を当てます。生物の複雑な営みを紐解いた背景や、それをアルゴリズムに落とし込むことで可能になった表現を紹介します。 本記事を読むことで日常に潜むあらゆる現象が芸術の種に見える喜びを感じていただければ幸いです。

サンプルはHTML CanvasとJavaScriptで作成しています。ソースコードは GitHubで公開 していますので、あわせてご参照ください。

ボイド

水族館でこのような魚の群れを見たことはあるでしょうか。

出典：「写真AC - ギンガメアジの群れ フィリピンバリカサグ島」

外から見る我々には秩序を持って行動しているように見えますが、魚たちの視界に映るのはきっと360度を囲む仲間たちです。彼らはどのようにこのようなパターンを形成しているのでしょう。
クレイグ・レイノルズは20世紀終わりにボイドという人工生命シミュレーションプログラムを作りました。このプログラムでは作成した個体クラスに3つの行動ルールを与えています。そのルールとは以下の3つです。

1. 他の個体と離れないこと
2. 他の個体と衝突しないこと
3. 全体の流れに沿って動くこと

このルールのもとでシミュレーションを行ったところ、集団はまさに動物の群れのような動きを見せたのです！ こちらがそのシミュレーションになります。

サンプルページと全体のソースコードへのリンクはこちらになります。

• サンプルを別ウインドウで開く
• ソースを見る

ソースコードの解説をします。それぞれの個体をBiontクラスとして作成し、他個体に応じて進行方向ベクトルを作成するメソッドを用意します。進行方向ベクトルは上記の条件1~3を満たすベクトルの和となります。

class Biont {
  constructor(x, y, vx, vy, id) {
    this.x = x; // 個体のx座標
    this.y = y; // 個体のy座標
    this.vx = vx; // 個体のx方向の速度
    this.vy = vy; // 個体のy方向の速度
    this.id = id; // 個体識別番号

    this.v1 = { x: 0, y: 0 }; // 条件1を表す速度ベクトル
    this.v2 = { x: 0, y: 0 }; // 条件2を表す速度ベクトル
    this.v3 = { x: 0, y: 0 }; // 条件3を表す速度ベクトル
  }
  update() {
    // 各ベクトルに適切な係数をかけて動きを調整します
    this.vx += 0.01 * this.v1.x + 0.8 * this.v2.x + 0.1 * this.v3.x;
    this.vy += 0.01 * this.v1.y + 0.8 * this.v2.y + 0.1 * this.v3.y;
    // ~ 省略 ~
    this.x += this.vx;
    this.y += this.vy;
  }
  draw() {
    // ~ 描画処理 ~
  }

  // 集団の中心に向かって移動します（条件1）
  getToCenterVector() {
    // ~ 省略 ~
  }

  // 仲間と近づきすぎたとき離れます（条件2）
  getAvoidanceVector() {
    // ~ 省略 ~
  }

  // 集団と同じ速度で動こうとします（条件3）
  getAverageVelocityVector() {
    // ~ 省略 ~
  }
}

条件1（中心に向かう）を表す関数getToCenterVectorでは自身以外の個体の平均の位置を計算し、そこに向かうベクトルを足しています

// 集団を格納する配列です
let boids = [];
// 集団の中心に向かうベクトルを返します  
getToCenterVector() {
  // 他の個体の座標の平均をcenterに代入します
  const center = { x: 0, y: 0 };
  boids
    .filter(biont => this.id !== biont.id)
    .forEach(biont => {
      center.x += biont.x;
      center.y += biont.y;
    })
  center.x /= boids.length - 1;
  center.y /= boids.length - 1;

  this.v1.x = center.x - this.x;
  this.v1.y = center.y - this.y;
}  

条件2（近づきすぎたら離れる）を表す関数getAvoidanceVectorでは他個体との距離が一定以下になったとき逆向きのベクトルを足しています。

// DIST_THRESHOLD内に仲間がいるとき逆向きのベクトルを返します  
getAvoidanceVector() {
  const DIST_THRESHOLD = radius;
  boids.filter(
    biont => dist(this.x, this.y, biont.x, biont.y) < DIST_THRESHOLD
  ).forEach(biont => {
    this.v2.x -= biont.x - this.x;
    this.v2.y -= biont.y - this.y;
  });
}

条件3（速度を周りに合わせる）を表す関数getAverageVelocityVectorでは自身以外の個体の速度ベクトルの平均を計算し足し合わせています。

// 集団と同じ速度で動こうとします  
getAverageVelocityVector() {
  // avgVに各個体の速度の平均を代入します
  const avgV = { x: 0, y: 0 };
  boids.filter(biont => this.id !== biont.id).forEach(biont => {
    avgV.x += biont.vx;
    avgV.y += biont.vy;
  });
  avgV.x /= boids.length - 1;
  avgV.y /= boids.length - 1;
  this.v3.x = avgV.x - this.vx;
  this.v3.y = avgV.y - this.vy;
}

以上の3つの速度ベクトルにそれぞれ適当な係数をかけて足し合わせ、フレームごとに各々の速度ベクトルを更新します。 更新はwindow.requestAnimationFrame()により行っています。

結果として、集団は群れのような動きを見せるのです。

遺伝的アルゴリズム

みなさんも知っての通り、多くの生物は二個体が交配し子を成します。生物は複数の遺伝子を持っており（人間の場合は約2万）、子はそれぞれの遺伝子を両親のどちらかから受け継ぎます。

似たような機能をもつ遺伝子にも個性があります。それは肌の色や血液型、お酒の強さにも現れていますよね。環境への適応度が低い遺伝子は淘汰され、より適応度の高い遺伝子のみが生き残ります。キリンの首が長い理由は、首を長くする遺伝子を持ったキリンの環境適応度が高かったからなのです。

ところで遺伝子の実態はどのようなものなのでしょう？　遺伝子は染色体と呼ばれる組織の上に配列状に存在しています。交配により染色体上の遺伝子のランダムな交換、「交叉」が発生します。
これによって、より多様な個体が生まれ、現在の環境に適した遺伝子をもつ個体が生存することができます。

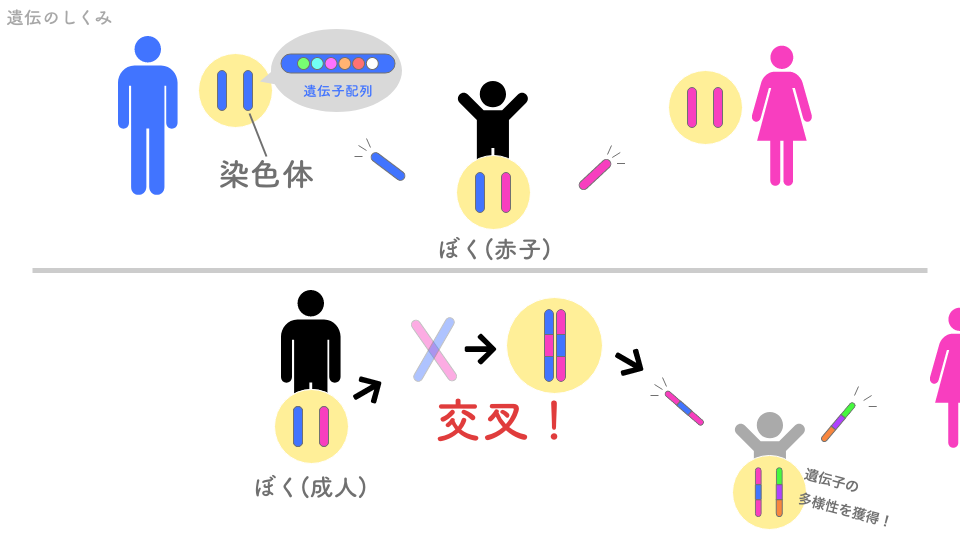
さらに染色体上の遺伝子は紫外線などのさまざまな条件によって「変異」を起こし異なる機能を獲得することもあります。これをシミュレーションしたものが遺伝的アルゴリズムになります。ルールは以下の通りです。

1. 現在の世代の集団から2個体を選択する
2. 選択した個体を交配させ子孫を生成。このときの遺伝子配列の交叉が起こる
3. 現在の世代で適応度の低かった個体を消去し2.の子孫を集団（次世代）に加える
4. 次世代の個体の遺伝子を一定の割合で変異させ、1に戻る

このアルゴリズムの特徴は最適解にたどり着く経路を効率良く探索できるところにあります。そのため、人工知能などにも用いられています。

遺伝的アルゴリズムを用いて作成したデモがこちらになります。

上に行くほど世代が進行します。環境適応度は一番上の色に近いほど高くなります。最初の世代はランダムな色が割り振られていますが、世代が進むにつれ環境に適応した個体、この場合は赤に近い個体が生き残っていることがわかります。

サンプルページと全体のソースコードへのリンクはこちらになります。

• サンプルを別ウインドウで開く
• コードを確認する

ソースコードに触れていきたいと思います。まず、現在の環境に最も適した遺伝子配列をgoalという配列で表現します。

// 適応度の基準の配列を作ります
let goal = [];
function createGoal() {
  // goalは[1, 1, 1, ...... , 1]となります
  goal = Array(360).fill(1);

  context.beginPath();
  context.fillStyle = `hsl(${genomeSize},50%,50%)`;
  context.rect(0, 0, canvas.width, 10);
  context.fill();
}

個体をBiontというクラスで定義し、goal配列との距離をgetEvaluateメソッドによって取得することでインスタンスの環境適応度を取得します。

class Biont {
  constructor(genome) {
    this.genome = genome;
  }
  // 適応度を取得します
  getEvaluation(goal) {
    let score = 0;
    for (let i = 0; i < this.genome.length; i++) {
      if (goal[i] === this.genome[i]) {
        score++;
      }
    }
    return score / this.genome.length;
  }
}

上記のルール1~4はそれぞれgetElite, getCrossedProgeny, getNextGeneration, getNextGenerationという関数で表現しています。

// 適応度の高い遺伝子をもつ個体をvalue体だけ返します
function getElite(age, value) {
  const elite = age.sort((a, b) => {
    return b.getEvaluation(goal) - a.getEvaluation(goal);
  });
  return elite.slice(0, value);
}

// 引数bios1, bios2の遺伝子配列を交叉させた子を返します
function getCrossedProgeny(bios1, bios2) {
  // bios1とbios2の遺伝子配列のcrossOne番目からcrossTwo番目を交換します。genomeSizeはインスタンス内のgenome配列の大きさです。
  const crossOne = Math.round(Math.random() * genomeSize);
  const crossTwo = crossOne + Math.round(Math.random() * (genomeSize - crossOne));
  const one = bios1.genome;
  const two = bios2.genome;
  const progenyOne = [
    ...one.slice(0, crossOne),
    ...two.slice(crossOne, crossTwo),
    ...one.slice(crossTwo, genomeSize)
  ];
  const progenyTwo = [
    ...two.slice(0, crossOne),
    ...one.slice(crossOne, crossTwo),
    ...two.slice(crossTwo, genomeSize)
  ];
  return [new Biont(progenyOne), new Biont(progenyTwo)];
}

// 次世代を作ります
function getNextGeneration(age, elite, progeny) {
  const sortedAge = age.sort((a, b) => {
    return a.getEvaluation(goal) - b.getEvaluation(goal);
  });
  sortedAge.splice(0, elite.length + progeny.length);
  sortedAge.push(...elite, ...progeny);
  return sortedAge;
}

// 遺伝子に変異を加えます。individualMutationRateは個体が変異する確率、genomeMutationRateは遺伝子の変異確率です
function mutate(
  age,
  individualMutationRate,
  genomeMutationRate
) {
  const boids = [];
  age.forEach(biont => {
    // 確率的に変異させる個体を選別します
    if (individualMutationRate > Math.random()) {
      const mutatedGenome = [];
      biont.genome.forEach(genome => {
        // 確率的に変異させる遺伝子を選別します
        if (genomeMutationRate > Math.random()) {
          mutatedGenome.push(Math.round(Math.random()));
        } else {
          mutatedGenome.push(genome);
        }
      });
      biont.setGenome(mutatedGenome);
      boids.push(biont);
    } else {
      boids.push(biont);
    }
  });
  return boids;
}

以上の処理をloop()関数内で行います。

let generation = 0;
let currentAge = [];
let newAge = [];
function loop(timestamp) {
  if (generation < 66) {
    // getElite
    const elite = getElite(currentAge, 2);
    // eliteの子供を作成
    const progeny = [];
    for (let i = 0; i < elite.length - 1; i++) {
      progeny.push(...getCrossedProgeny(elite[i], elite[i + 1]));
    }
    // elite, progeny, 現在の世代から適応度の高い順に選別
    newAge = getNextGeneration(currentAge, elite, progeny);
    // 適度に変異を入れる
    newAge = mutate(
      newAge,
      INDIVIDUAL_MUTATION,
      GENOME_MUTATION
    );
    // 描画
    newAge.forEach((age, index) => {
      // =========================描画処理=============================
    });
    generation++;
    // 次世代を現世代に
    currentAge = newAge;
    newAge = [];
  }
  window.requestAnimationFrame(ts => loop(ts));
}
window.requestAnimationFrame(ts => loop(ts));

以上の処理を行うことによって、世代が進むにつれ適応度の高い集団が形成されます。

セル・オートマトン

ライフゲームと呼ばれる言葉を耳にしたことはあるでしょうか。平面上にあるドットが周囲の環境に応じて誕生、進化、淘汰などの振る舞いを見せるシミュレーションです。これは生きるためには過密でも過疎でもダメ、という点が細菌などの生物の繁殖を模倣しているとも言われています。

このように、近傍の状態を受けて状態が変化していく計算モデルを「セル・オートマトン」と呼びます。ライフゲームは2次元のセル・オートマトンの代表的な例です。

自然界でもこの計算モデルに即した現象がいくつか見られます。たとえばイモガイの貝殻の模様がそれにあたります。これは色素をもつ細胞が活性化されると周囲の細胞の色素を不活性化して天然のセル・オートマトンのようにふるまうからと言われています。

• 「貝の図鑑」　タガヤサンミナシ- イモガイ科 -

話をライフゲームに戻します。黒いセルの状態を「生」、白いセルの状態を「死」と定義するとそれぞれのセルは以下のルールに従っています。

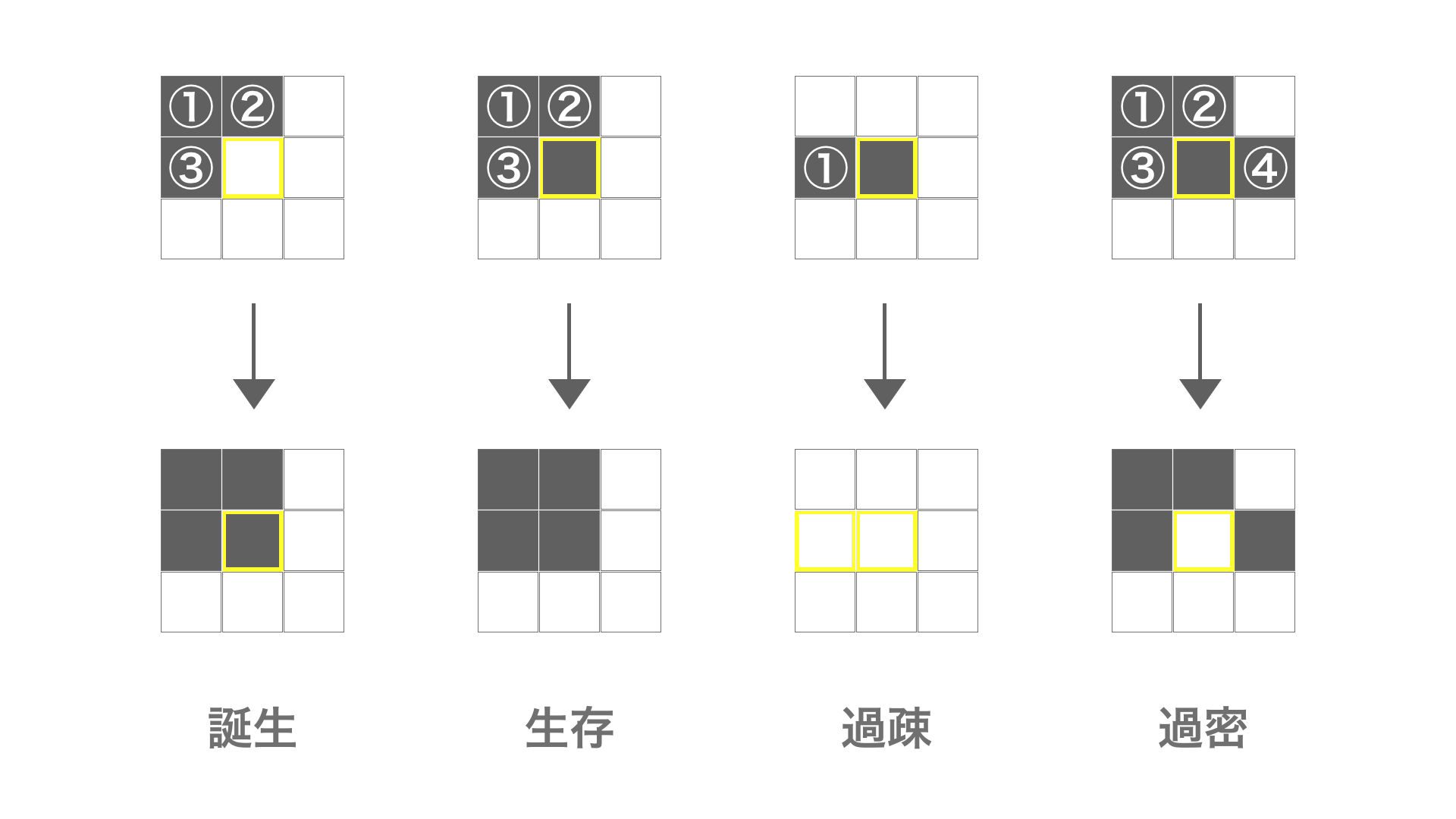
• 誕生：死んでいるセルに隣接する生きたセルが3つあるとき、誕生する
• 生存：生きているセルに隣接する生きたセルが2つまたは3つあるとき、そのまま生存する
• 過疎：生きているセルに隣接する生きたセルが1つ以下のとき、死滅する
• 過密：生きているセルに隣接する生きたセルが4つ以上のとき、死滅する

このルールのもと、初期状態を変えることでさまざまなセルのパターンを見ることができます。

実装は、さまざまなサイトで紹介されているのでそちらを検索していただいても構いません。今回は例の一つとして紹介します。サンプルページと全体のソースコードへのリンクはこちらになります。

• サンプルを別ウインドウで開く
• ソースを確認する

cellという二重配列を作成し値がALIVEのときは生存、DEADのときは死亡とします。proceed関数内ではcheckAround関数で周囲の生存しているセルの数を取得し、その数に応じて次の状態を決定しています。この処理をsetInterval(proceed, 100)により、100ミリ秒ごとに繰り返しています。

// ループごとにセルの状態を変える関数
function proceed() {
  for (let col = 0; col < cols; col++) {
    for (let row = 0; row < rows; row++) {
      // 周りの生存セルの数を取得
      const count = checkAround(col, row);
      const currentState = cell[col][row];
      let nextState = DEAD;
      // 生存時に周りに2体いるときは維持
      if (count === 2) {
        nextState = currentState;
      }
      // 周りに3体いるときは誕生または維持
      if (count === 3) {
        nextState = ALIVE;
      }
      cell[col][row] = nextState;
    }
  }
  // 画面の更新
  draw();
}

ライフゲームでは特定のパターンをもつセルの集合は周期的な動きを見せることがあります。LifeWiki というwebサイトでは無数の周期的なパターンがまとめられているので、興味を持った方はぜひご覧ください。

また、Golly というアプリケーションでは大規模なライフゲームのサンプルが豊富に用意されています。こちらも合わせてお試しください。

終わりに

今回紹介できなかったパターンとして、シマウマの模様のようなパターンを作るチューリングパターンなどまだまだ生物から学べる表現はたくさんあります。さらに生物だけでなく自然科学の中には表現のヒントになる現象がたくさん潜んでいます。

また、ICS MEDIAではジェネラティブアートのチュートリアルとして以下の記事も掲載しております。みなさんとともに作品を見せ合えるる日を楽しみにしています！

• JavaScriptで取り組むクリエイティブコーディング - パーティクル表現入門
• JavaScriptで取り組むクリエイティブコーディング - パーリンノイズを使いこなせ