WebGL開発に役立つベクトルの外積（Three.js編）

2022年5月27日更新 / 株式会社ICS

この記事は前回の「WebGL開発に役立つベクトルの内積 (Three.js編)」の続編です。前回はベクトルの内積を勉強しましたが、今回は外積について紹介します。外積は高校までの数学では学んでいないと思いますが、本記事では簡潔に要点だけを解説するので安心してください。外積は衝突判定や、光の表現など、3Dコンテンツ制作において重要なさまざまな場面で活躍します。一緒に外積について学び、外積をThree.jsでどう応用していくかを学んでいきましょう。

外積を使った3Dのデモの紹介

本題に入る前に外積を使ったデモを作成したので紹介します。今回は以下のようなトロッコがレールに沿って走る処理を外積を使って実装しています。サンプルコードもGitHubにアップしているので参考にしてください。

※このデモはThree.js(r141)で作成しています。

外積

外積とは

外積は内積と同じくベクトルの掛け算ですが、内積はスカラーが求まるのに対し、外積はベクトルが求まります。さらにそのベクトルは2つのベクトルに垂直になるという性質を持ちます。

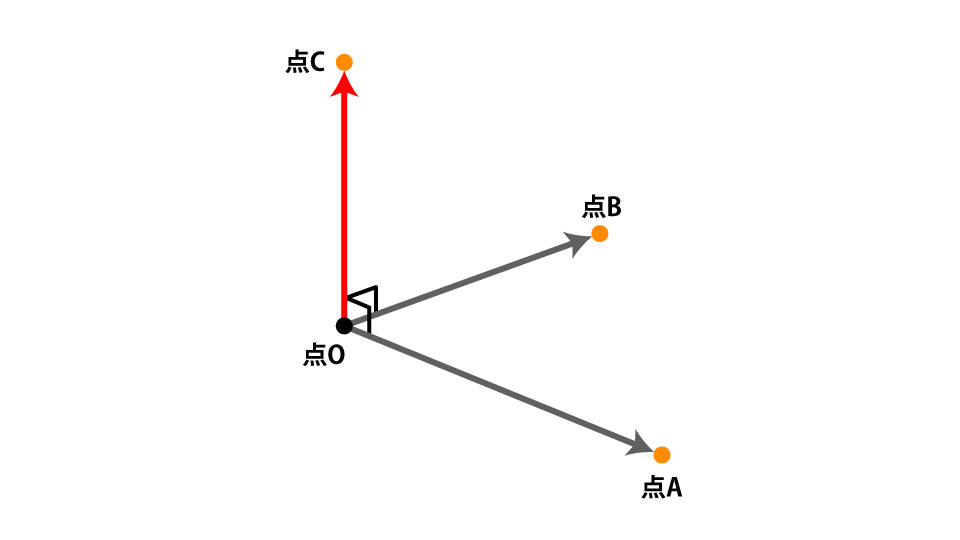
図のようにOAベクトルとOBベクトルがある時、2つのベクトルの外積はOCベクトルになります。OCベクトルはOAベクトルとOBベクトルの二辺からなる平面に対して垂直なベクトルです。

数式では外積はOA x OBのようにクロス繋ぎで表記します。今回のOCベクトルを式で表すと以下のようになります。

OA x OB = OC

OAベクトルとOBベクトルに垂直なベクトルはOCベクトルだけでなく、OCベクトルの反対向きのベクトルもありますが、今回の場合はOCベクトルが外積となります。それは、外積のベクトルの方向は式の書き順によって決定するからです。

今回の例で解説すると、点Oを軸にOAベクトルをOBベクトルへ移動するようにネジを回した時に動く進む方向が外積の向きになります。よって、式のOAベクトルとOBベクトルを入れ替えれば、外積はOCベクトルの反対向きのベクトルになります。

外積の長さ

では外積で求めたOCベクトルとはどのような長さになるでしょうか？ 実はOAベクトルとOBベクトルの二辺からできる平行四辺形の面積が、そのままOCベクトルの長さになるという性質を持ちます。平行四辺形の面積を求める式は

面積 = 底辺 * 高さ;

でしたね。よって|OA|を底辺とした時、高さは|OB|sinθとなるので|OC|を求めるには以下の式になります。

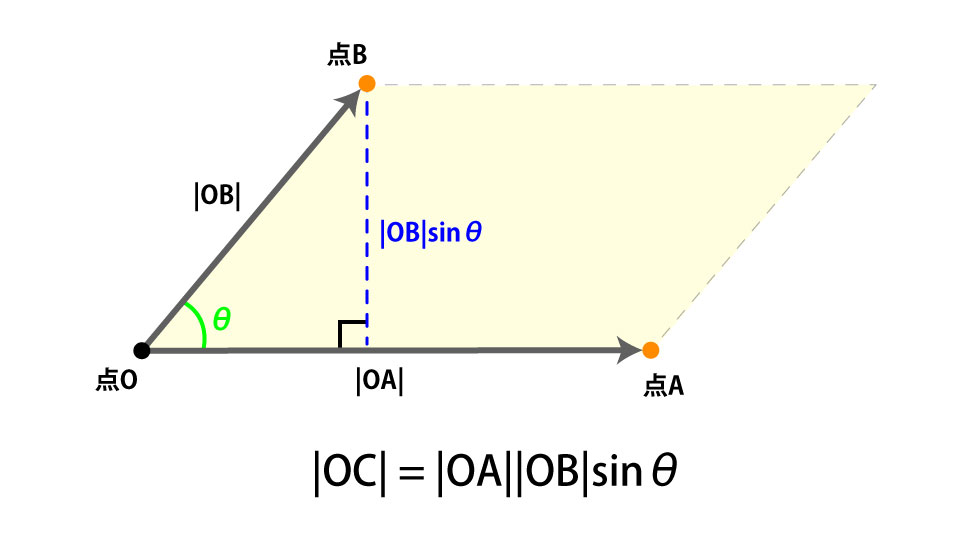
この外積の長さの性質について本記事のデモでは使用しませんが必ず覚えておきましょう。

Three.jsでの外積の計算

Three.jsで外積を計算する場合は、THREE.Vector3クラスに用意されているcross()メソッドを使用します。以下のコードはOCベクトルを求める為のものです。

const vOA = new THREE.Vector3(0, 0, 1);
const vOB = new THREE.Vector3(1, 0, 0);
const vOC = vOA.cross(vOB);

外積を使ってデモを作成してみよう

冒頭で紹介したデモを実装する為のポイントを解説します。

ステップ1. コースを作ろう

まずはトロッコを走らせる為のコースを作りましょう。三角関数を使い円形に360分割した点を作成します。

// 座標リスト
const points = [];
// 半径
const radius = 5;

// 円形に360分割した点を格納
for (let index = 0; index < 360; index++) {
  const rad = (index * Math.PI) / 180;
  const x = radius * Math.cos(rad);
  const y = radius * Math.sin(rad);
  points.push(new THREE.Vector3(x, y, 0));
}

この作成した点の上をトロッコが走ります。記事冒頭のデモはコースをわざと歪ませています。上の式を変更すればコースの形も変わるので自分好みのコースに変形してみてください。

※画像は分かりやすくするためコースを可視化しています。

ステップ2. トロッコをコースに沿って動かそう

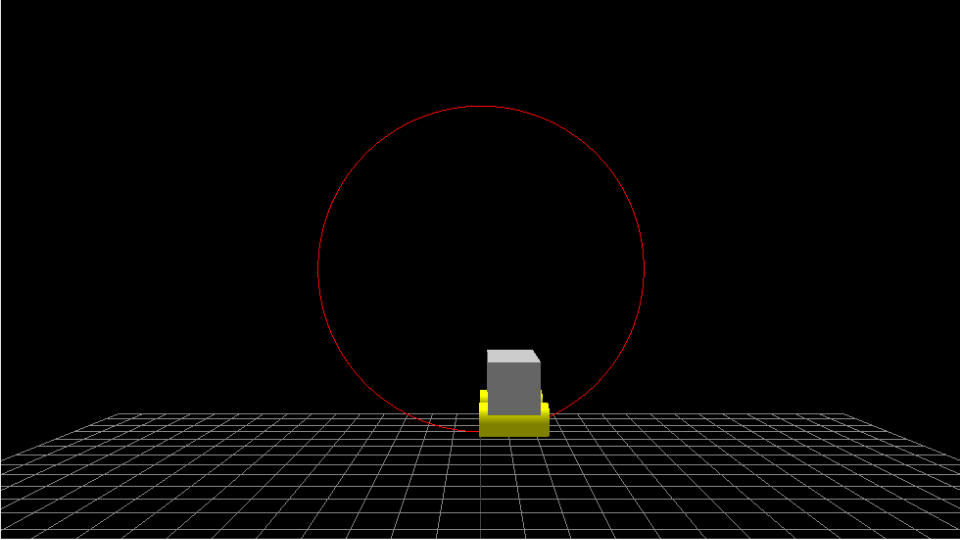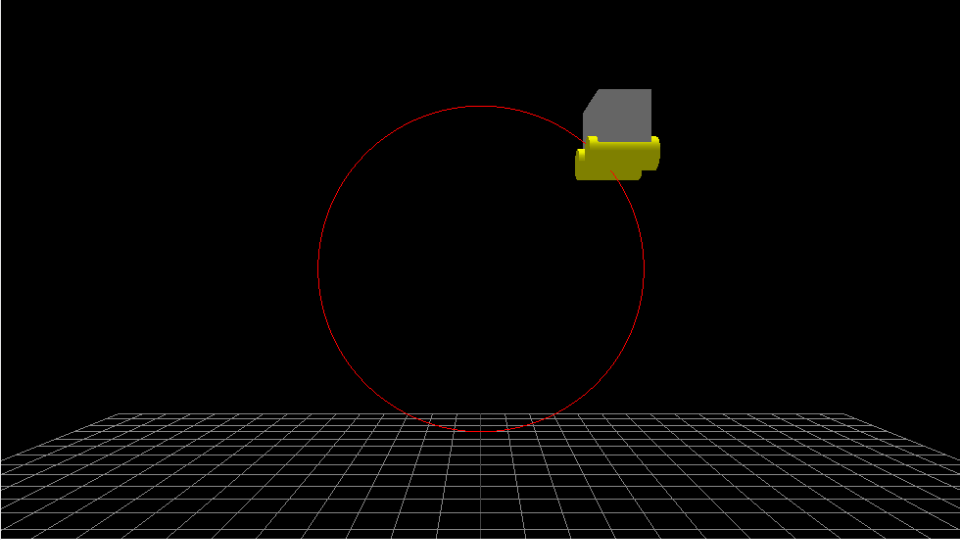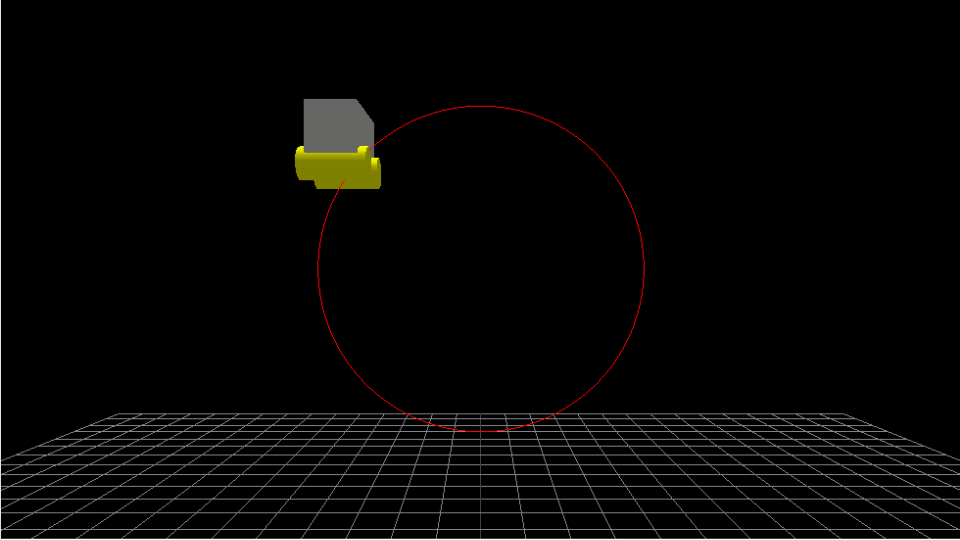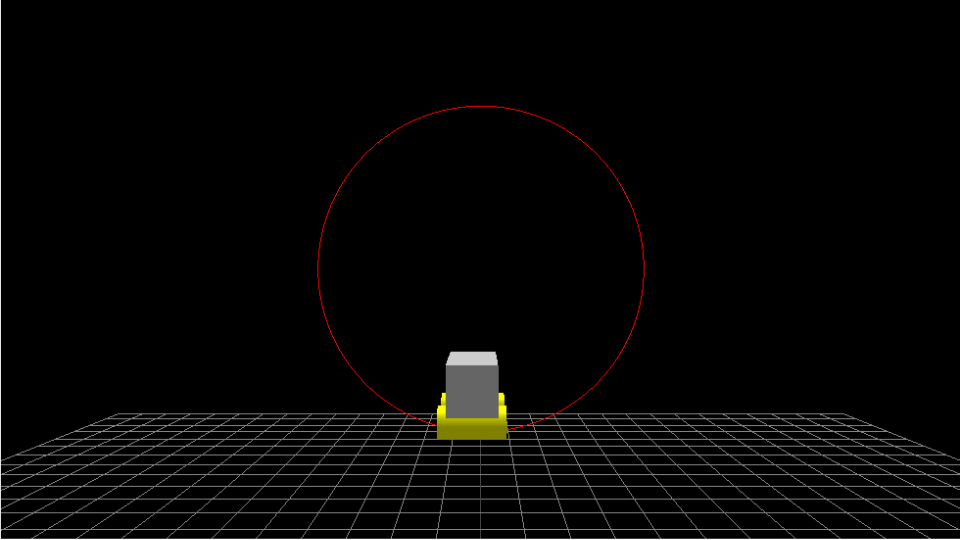
ステップ1で作成したコースに沿ってトロッコを動かしてみます。この時truck変数にはトロッコのメッシュが代入されており、update()関数は毎フレーム実行されるものとします。

// フレーム数
let frame = 0;
// アニメーションの開始時間を格納する変数
const startTime = Date.now();
// フレーム毎に更新します。
function update(startTime) {
  // 現在時間の継続時間に対する進捗度を算出
  const progress = (Date.now() - startTime) / 6000;
  // 6秒かけて1周する（コースを360分割した点を移動）
  frame = Math.round(360 * (progress - Math.floor(progress)));
  // トラックの位置を修正
  truck.position.copy(course.points[frame]);
}

update()関数内で開始時刻からの経過時間に応じたトラックの移動量を計算し、その移動量に合ったインデックスの座標をトラックの位置としてフレーム毎に設定しています。

ステップ3. トロッコの向きを修正しよう

ステップ2でコースに沿ってアニメーションできるようになりましたが、トロッコとしては不自然なアニメーションです。コースに合わせてトロッコの向きが変わるように修正してみましょう。

トロッコの向きを直すにはコースの法線ベクトルを使用します。法線とは面に直角に交わるベクトル、すなわち面の向きを表すベクトルを意味します。今回のコースの法線ベクトルは以下のようなベクトルの事を指します。

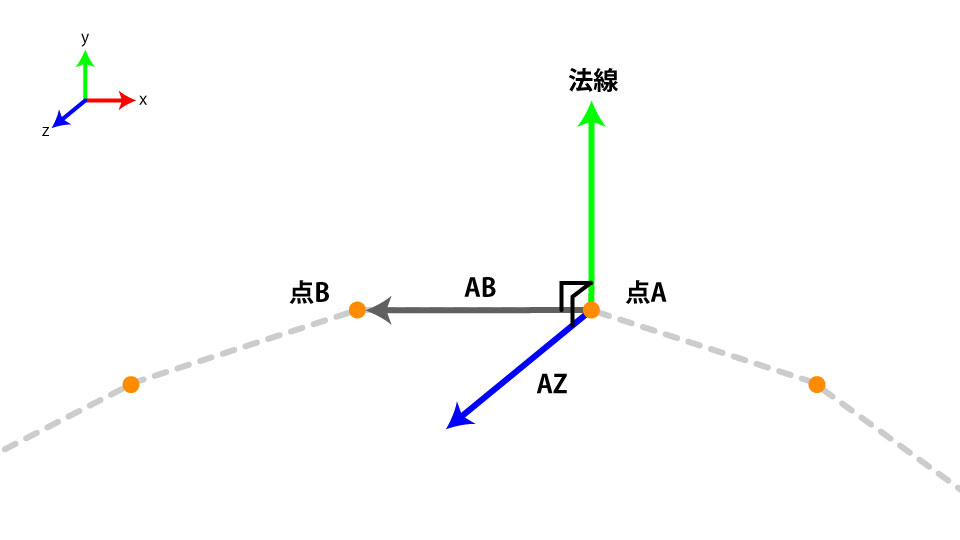
法線ベクトルを求めるには、現在位置（点A）と次フレームの位置（点B）を結んだベクトルであるABベクトル、z向きの単位ベクトルであるAZベクトルの外積から求めることができます。JavaScriptの関数で表すと以下のようなコードになります。

// 現在位置と次フレームの位置から法線を算出します。
function getNormal(currentPoint, nextPoint) {
  const vAB = nextPoint
    .clone()
    .sub(currentPoint)
    .normalize();
  const vAZ = new THREE.Vector3(0, 0, 1);
  const normalVec = vAB.cross(vAZ);

  return normalVec;
}

次に、算出した法線ベクトルをトロッコの上向きベクトルとして設定します。上向きベクトルはTHREE.Meshクラスのupプロパティをset()メソッドを使用して設定できます。

// トロッコの上向きベクトルを更新
truck.up.set(normal.x, normal.y, normal.z);

しかし、上向きベクトルを更新しただけではオブジェクトの見た目には反映されません。上向きベクトルの設定を反映させるにはlookAt()メソッドを呼ぶ必要があります。

// トロッコのlookAtを更新
truck.lookAt(course.points[frame + 1]);

lookAt()メソッドは引数として渡した位置ベクトルの方向にオブジェクトが向きを変えます。しかし、向きを変える際に頭がどの方向にあれば良いかわからないため、さきほどのupプロパティに設定した上向きベクトルを使用してオブジェクトの姿勢を決めます。ようやくトロッコが正しい向きでコース上を走行するようになりました。

終わりに

外積の性質を応用することで法線ベクトルを算出できる事が分かりました。3Dコンテンツを制作する上で、頻繁に法線ベクトルを求めなければならない場面に出くわします。今回のデモではオブジェクトの上向きベクトルとして使用しましたが、あくまで一例にすぎません。本記事で基本的な外積の使用方法を知ることができたので、今後の皆さんの3Dコンテンツ制作ではどこで応用可能かを探してみるといいと思います。また、前回までに学んだ内積や足し算・引き算も併せて活用できれば表現の幅が広がるはずなので、是非チャレンジしてみてください。