WebGL開発に役立つベクトルの足し算・引き算（Three.js編）

2022年5月27日更新 / 株式会社ICS

みなさんベクトルをプログラムで活用していますか？　学校で学んで以来、縁が無くなった方も多いかと思いますが、実は3Dコンテンツの制作においてベクトルは役に立つ概念なんです。本記事ではThree.jsとベクトルの基礎である足し算・引き算を使った座標の計算方法を紹介します。

ベクトルと聞くだけで拒絶するエンジニアもいると思いますが、心配いりません。Three.jsが煩わしい計算をすべておこなってくれるので、ベクトルの性質だけ覚えれば誰でも扱えるようになります。基本からおさらいし、実際にThree.jsでどのようにベクトルを扱っていくか学んでいきましょう。

ベクトルを使った3Dのデモの紹介

本題に入る前にベクトルを使ったデモを作成したので紹介します。今回は以下のような物体を追従するカメラをベクトルを使って実装しています。サンプルコードもGitHubにアップしているので参考ください。

※このデモはThree.js(r140)で作成しています。

ベクトルのおさらい

ベクトルを知っている人も知らない人もベクトルおさらいをしましょう。まずは3次元ではなく二次元で解説します。

そもそもベクトルとは？

ベクトルは向き、量の2つの情報を持っています。矢印でイメージする場合、矢印の向きが向き情報、長さが量を示します。

位置ベクトル

本来ベクトルは位置情報を持っていませんが、原点(0, 0)から伸びているベクトルは座標を示す事ができるため、そういったベクトルを位置ベクトルと言います。

ベクトルの足し算

点O(0, 0)、点A(2, 0)、点B(1, 1)の三点が存在するとします。この時、点Oから点Aを結ぶベクトルをOAベクトルとし、点Oから点Bを結ぶベクトルをOBベクトルとします。この時OAベクトルとOBベクトル足すと以下の図のようなOCベクトルになります。

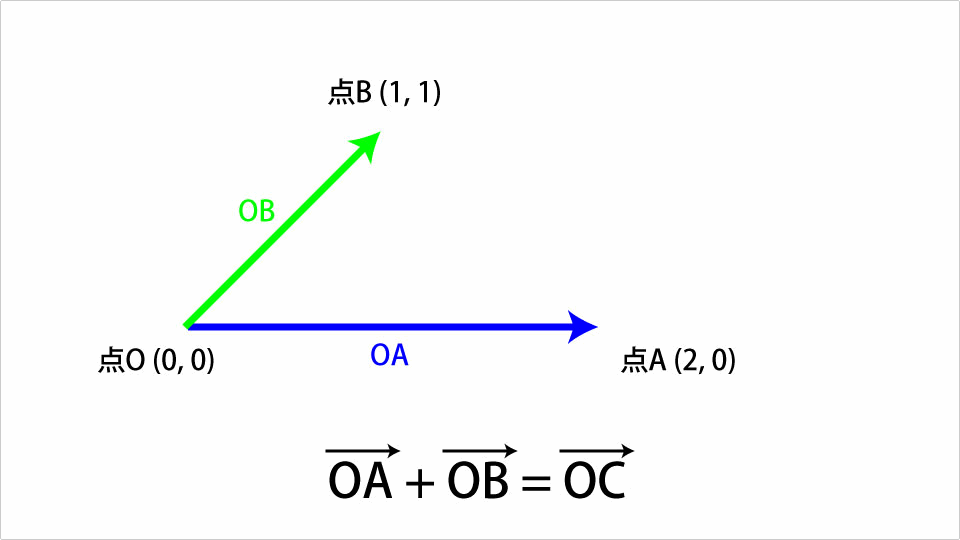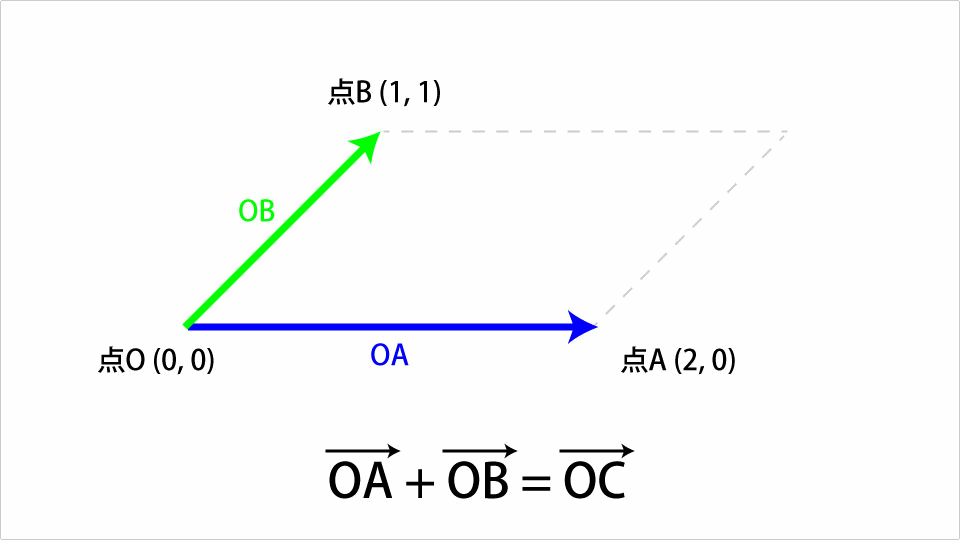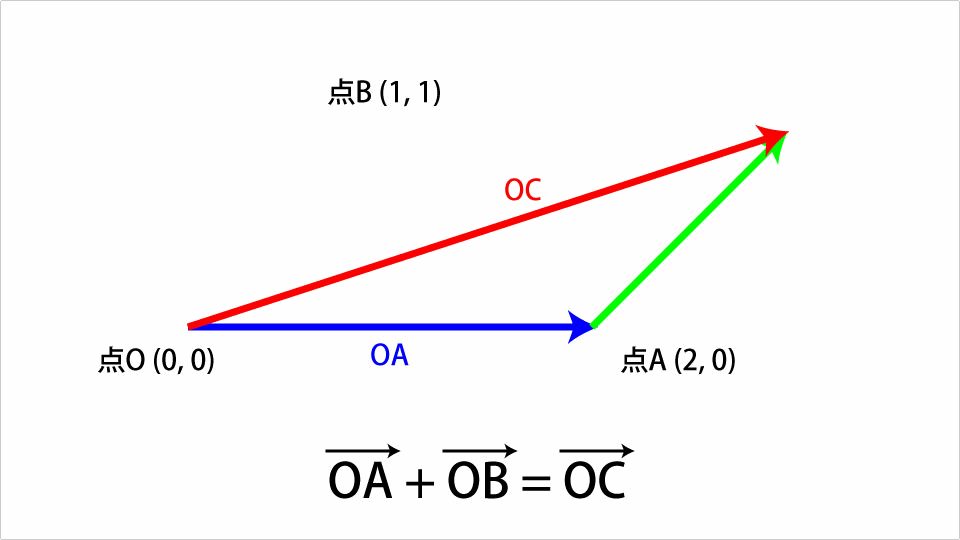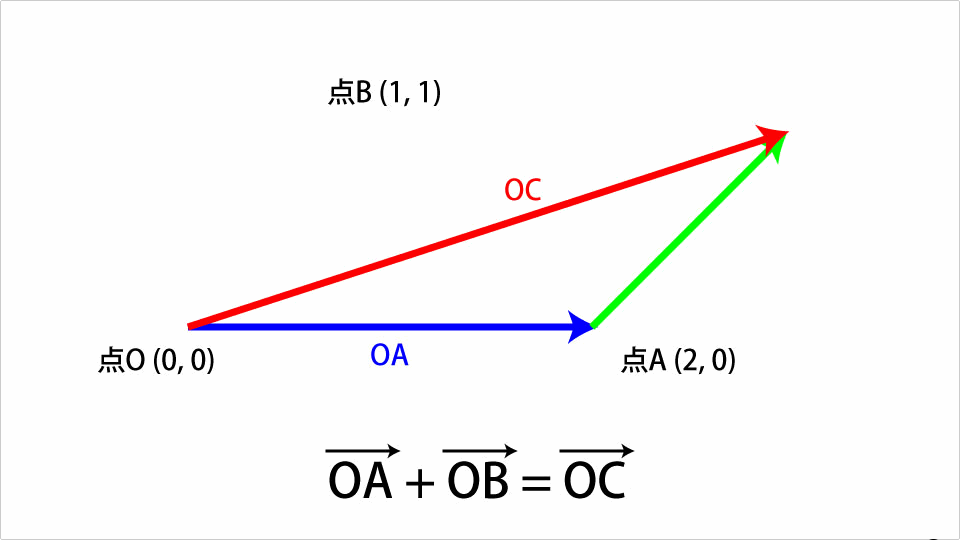
OBベクトルをOAベクトルの先端までずらし、その時のOAベクトルの開始点とOBベクトルの先端を結ぶベクトルが和になります。これをThree.jsを使ったコードで表すと以下のようになります。

const vOA = new THREE.Vector2(2, 0);
const vOB = new THREE.Vector2(1, 1);
const vOC = vOA.add(vOB);

和を求める場合はTHREE.Vector2クラスに用意されているadd()メソッドを使います。

ベクトルの引き算

足し算の時と同様のOAベクトルとOBベクトルで考えていきます。OAベクトルからOBベクトルを引くと以下のようなOCベクトルになります。

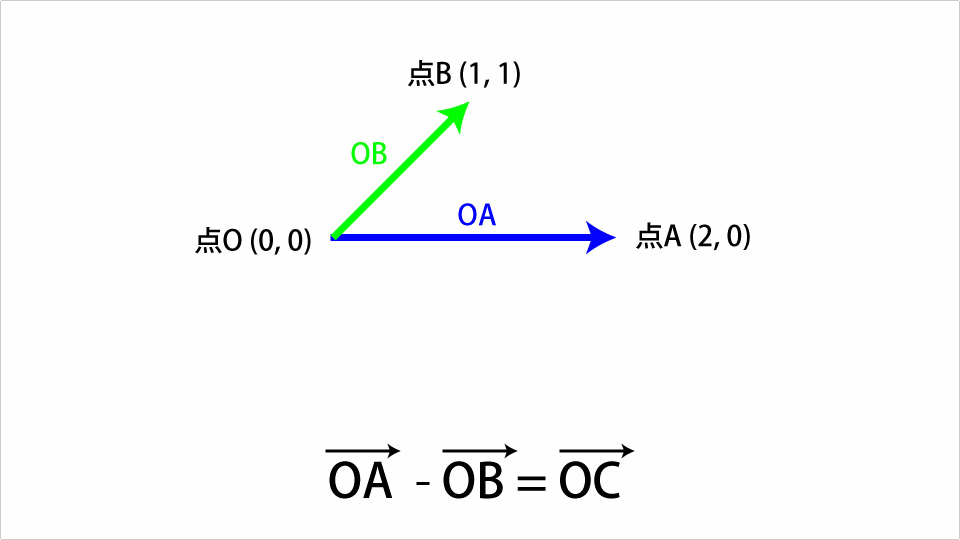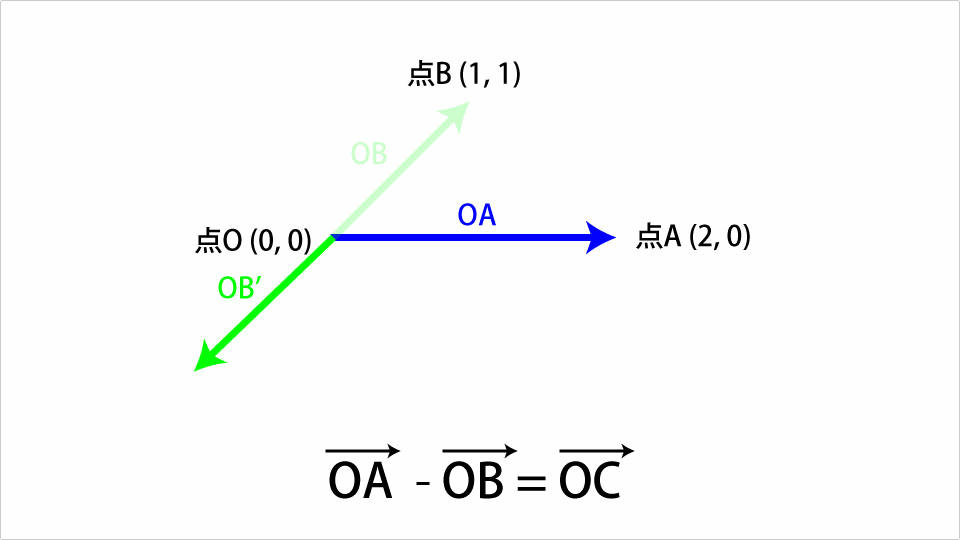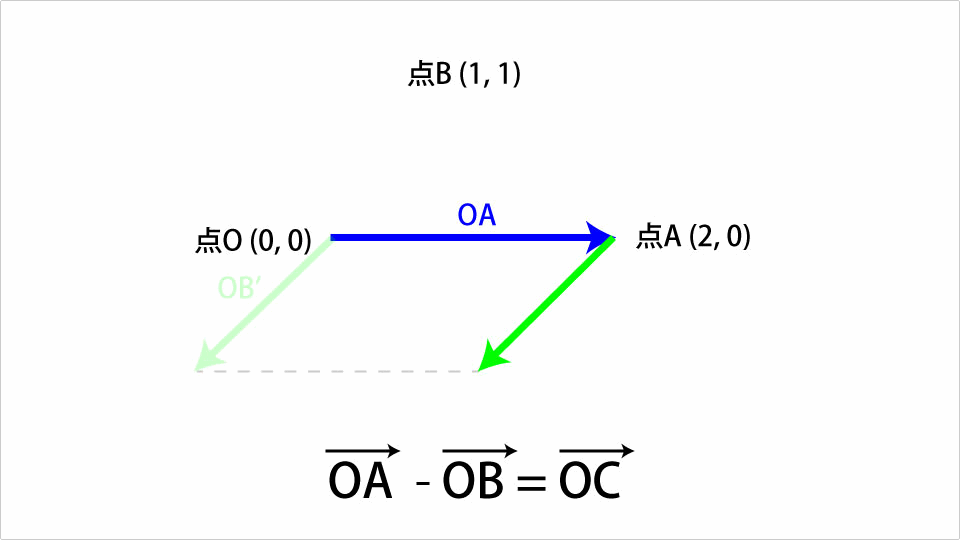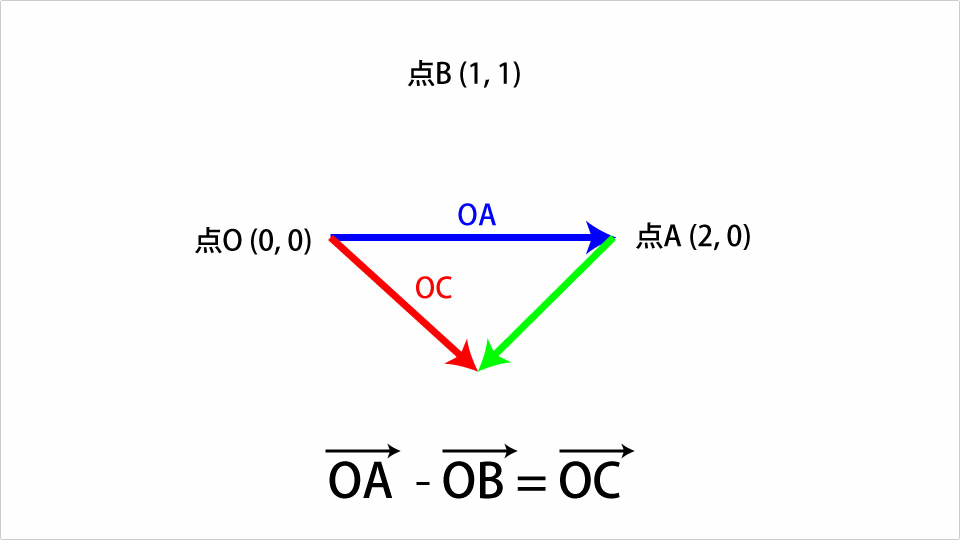
引き算の場合はまずOBベクトルの向きを反転させます。あとは足し算と同様の考え方で差を表現できます。これをThree.jsを使ったコードで表すと以下のようになります。

const vOA = new THREE.Vector2(2, 0);
const vOB = new THREE.Vector2(1, 1);
const vOC = vOA.sub(vOB);

差を求める場合はTHREE.Vector2クラスに用意されているsub()メソッドを使います。

Three.jsでベクトルを使ってみよう

Three.jsとベクトルを使った、実践的なコードを確認していきましょう。以下の2つのステップに分け順に解説します。

動きまわる球の正面ベクトルを求めてみよう
球の後ろにカメラを追従させよう

ここからは3次元ベクトルを扱いますが、二次元の時とほぼ同じなので心配はいりません。

ステップ1: 動きまわる球の正面ベクトルを求めてみよう

円運動しているsphereという球状のメッシュがあるとします。球の前方を表すベクトルを求めるには移動前と移動後の位置ベクトルの差を使います。以後本記事では前方を表すベクトルを正面ベクトルと呼びます。

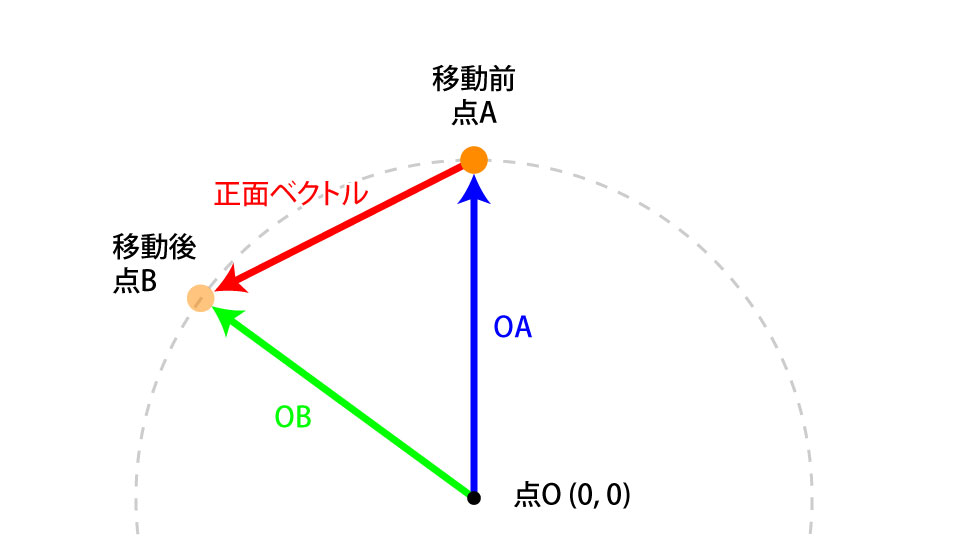
OBベクトルからOAベクトルを引いたものが球の正面ベクトルになります。前項の引き算の説明では原点から伸びるベクトルを導き出していましたが、ここでは点Aからの向きを表すベクトルとしたいため、上の図では点Aを始点とするようにベクトルを移動させています。仕組みが分かったのでThree.jsのコードを書いていきましょう。

まずは移動後と移動前の座標を取得します。getNewPosition()は円運動の次の位置情報（THREE.Vector3）を返却するものとします。

// 現在の位置を保持しておく
const oldPosition = sphere.position.clone();
// アニメーション後の新しい位置を取得
const newPosition = getNewPosition();

newPositionとoldPositionの差を求めます。

// newPosition - oldPostionで進んでいる方向のベクトルを算出
frontVector = newPosition.clone().sub(oldPosition);

ここまでで正面ベクトルは求まりましたが、今回のように大きさの情報が必要ないような場合は、単位ベクトルへ直しておくと後々扱いやすくなります。単位ベクトルとは長さが1のベクトルの事を指します。最後にnormalize()メソッドで単位ベクトルへ変換しておきましょう。単位ベクトルに変換することを「正規化せいきか（英語ではNormalizeノーマライズ）」と言います。

// 単位ベクトルに変換
frontVector = frontVector.normalize();

ここまでの処理を毎フレーム行い正面ベクトルを更新すればStep1の完成です。

※ このプレビューはTHREE.ArrowHelperを使ってベクトルを可視化しています。

ステップ2: 球の後ろにカメラを追従させよう

カメラの位置の計算にはさきほどの球の正面ベクトルを用います。仕組みとしては球の背後に一定距離離した位置にカメラが来るように計算します。

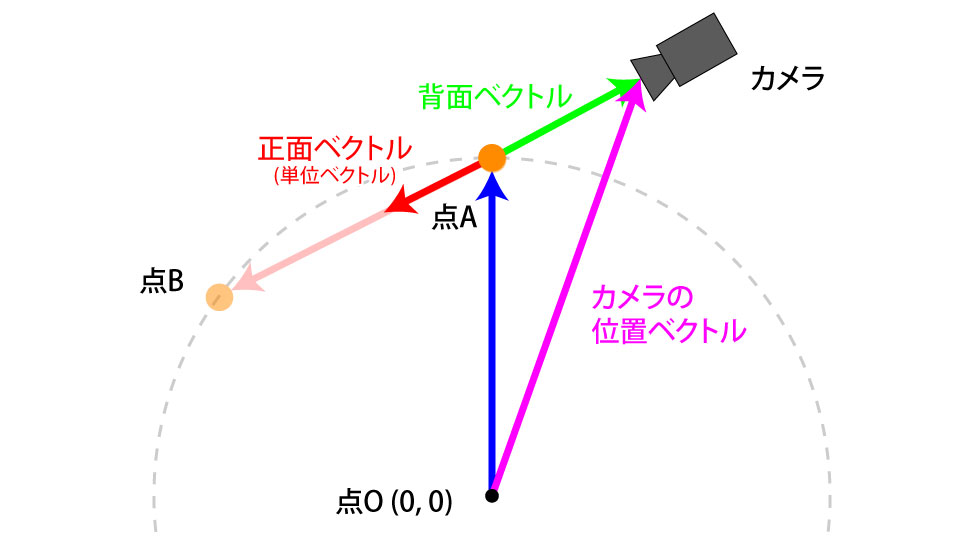
まず球の正面ベクトルの逆向き、つまり背面ベクトルを計算します。THREE.Vector3クラスのnegate()というベクトルを反転させるメソッドを使用します。この時、正面ベクトルを変更してしまわないようにclone()メソッドを挟んでおきます。

// 背面ベクトル
const backVector = frontVector.clone().negate();

背面ベクトルはすでに単位ベクトルとなっているので、球とカメラを離したい分だけ伸ばします。multiplyScalar()メソッドを使って拡縮をしてみましょう。

// 球とカメラの距離
const distance = 10;
// 背面ベクトルを距離分引き伸ばす
backVector.multiplyScalar(distance);

球の位置ベクトルを足しカメラの位置を求め、位置を更新します。

// カメラ位置を算出
const cameraPosition = backVector.add(sphere.position);
// 算出したカメラ位置を反映
camera.position.copy(cameraPosition);

このままではカメラが球の方向を向いていないので、lookAt()メソッドを使いカメラの向きを修正します。

// カメラを球に向かせる
camera.lookAt(sphere.position);

これで球にカメラが追従するようになりました。この処理だけでFPSゲーム風なカメラアングルになったかと思います。意外と仕組みが分かってしまうと簡単ですね。

終わりに

ベクトルが座標計算に役に立つ事がわかっていただけたのではないでしょうか？　今回はベクトルの足し算と引き算に絞った解説でしたが、内積や外積を使用することでもっと複雑な動きや処理が可能になります。本記事でベクトルがなんとなく理解できたという方は内積と外積にも是非挑戦してみてください。

また、記事「WebGL開発に役立つ重要な三角関数の数式・概念まとめ」ではThree.jsと三角関数を使った表現の解説もしているので併せて参考ください。

この記事は「Three.js入門サイト」連載の1つです。

ICS MEDIA