普段、みなさんはプログラムでデータのソートをするとき、内部でどのようなアルゴリズムが働いているか意識していますか? 大半の方はプログラム言語にあらかじめ用意されているソート関数を使用し、特別にアルゴリズムについて意識することは少ないと思います。ソートのアルゴリズムにはデータ量やデータの初期の状態に応じた向き不向きがあり、それぞれのアルゴリズムについての理解を深めて適したものを選択すると、ソートにかかる時間を短縮できることがあります。
ソートアルゴリズムの可視化デモ (HTML5製)
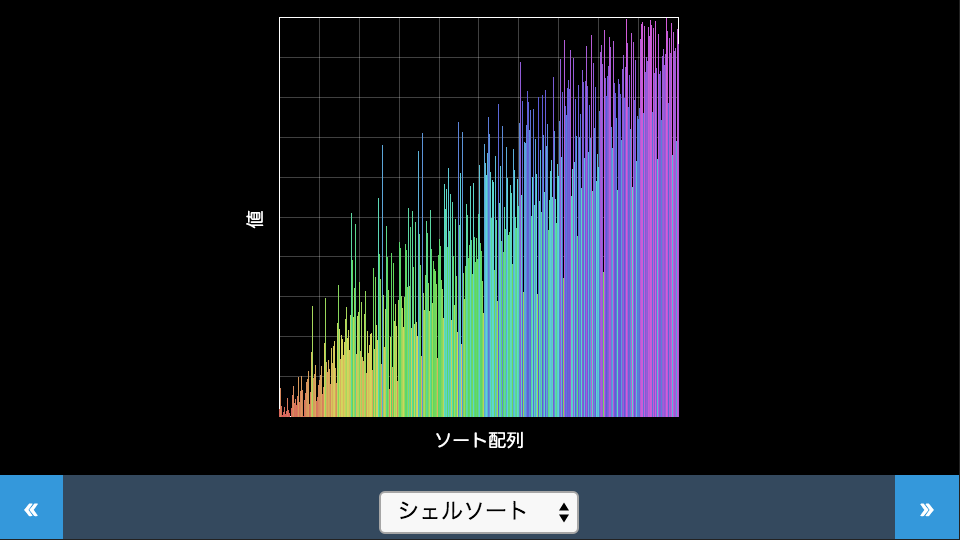
次のデモはソートのアルゴリズム可視化するコンテンツです。HTML5 Canvas要素とJavaScriptで作成しています。画面下のプルダウンでアルゴリズムの種類を選択すると、ランダムに配置されたデータが選択した方式に応じたアルゴリズムでソートされる様子を表示します。
※デモ中のソートが完了するまでの時間と実際のソート速度に相関はありません。
※このデモはCreateJS 2015年11月版とTypeScript 1.8で開発しています。
以下にデモ中で使用しているそれぞれのソートの特徴に筆者の主観によるオススメ度を加えて解説します。
要素数について
ソート処理にかかる平均の時間を平均計算時間と呼び、O(n^2)のように、ソート対象の要素数nの式でO(オー)という記号で表します。一般に要素数nが増えるにつれてソートにかかる時間は増えますが、時間の増え方の概算(オーダー)を表現することができ、要素数から適したソートアルゴリズムを比較、選択する際の目安になります。
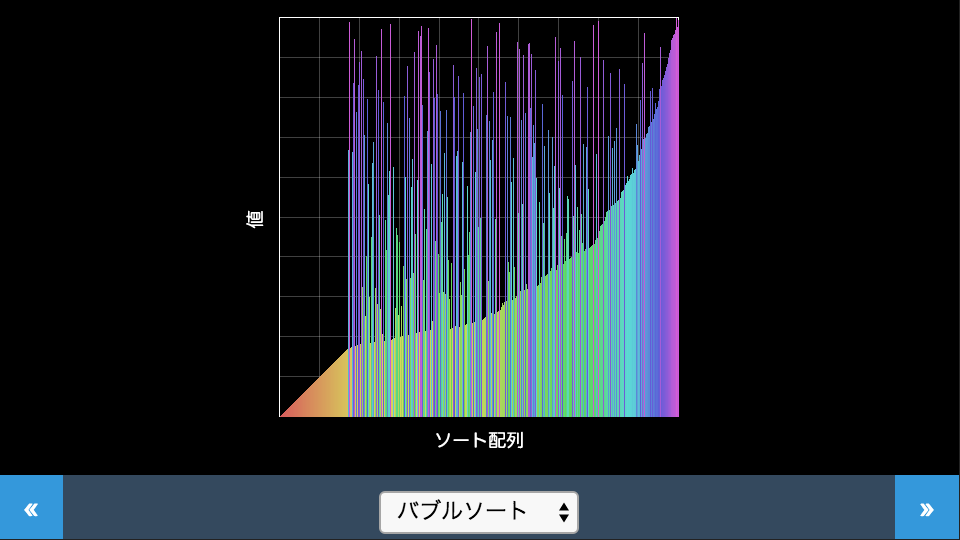
バブルソート
アルゴリズム
末尾から隣り合った要素を順に比較し、小さい方が先になるよう交換します。比較が先頭まで終了すると一番小さな値が先頭になるので、次は先頭から2番目の値を探してまた末尾から順に比較する作業を繰り返します。泡(バブル)のように要素が移動していくことが名前の由来です。デモでは要素が右に移動していき、左から位置が確定していく様子が見られます。
計算量
比較交換回数が非常に多く、平均計算時間はO(n^2)となり、ソートのアルゴリズムとしては遅い部類です。
オススメ度
★★★☆☆(3)
もっとも基本的で遅いソートとして知られていますが、それだけにソースコードは単純で理解がしやすく、要素数が数十程度の軽いソートの場合はバブルソートをオススメします。
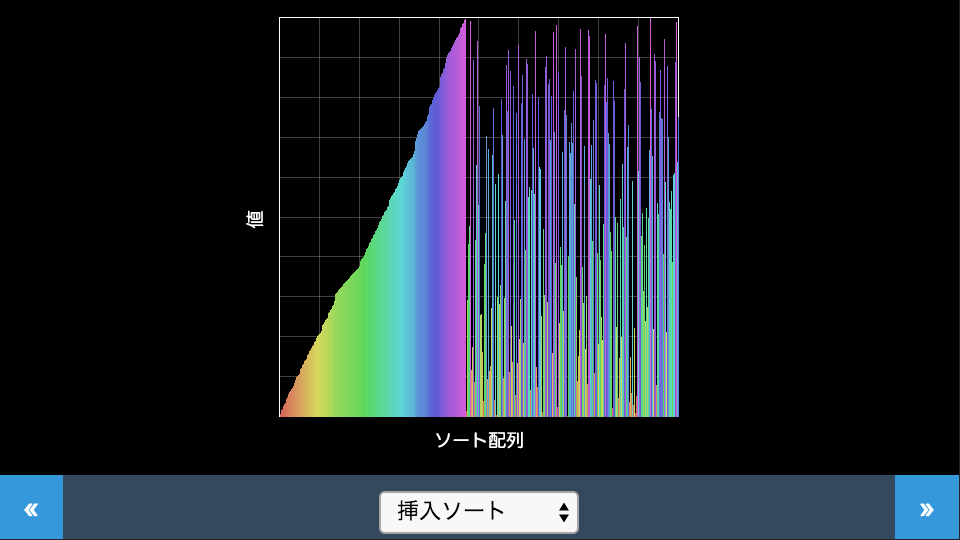
挿入ソート
アルゴリズム
まず1番目と2番目の要素だけで考え、値の小さな順になるよう並び替えます。次に3番目の要素を1,2番目のデータ列に対して順番が適切な位置になるよう挿入します。3番目のデータまでの順番は整列された状態になるので、以降4番目、5番目と整列済みのデータ列に対して適切な位置になるよう挿入します。デモでは注目する値が1番目から順番に整列済みデータに挿入されていき、左からだんだん整列済み領域が拡大していく様子が見られます。
計算量
比較がnの2重ループになるため、平均計算時間はO(n^2)となります。
オススメ度
★★★☆☆(3)
バブルソートと同じくO(n^2)の比較のため要素数が多くなると平均計算時間は加速度的に遅くなります。しかし、挿入ソートはすでにほとんどソートされた状態のデータ列に対しては高速に動作することが知られており、そのような場合にオススメです。また、ソースコードも単純です。
選択ソート
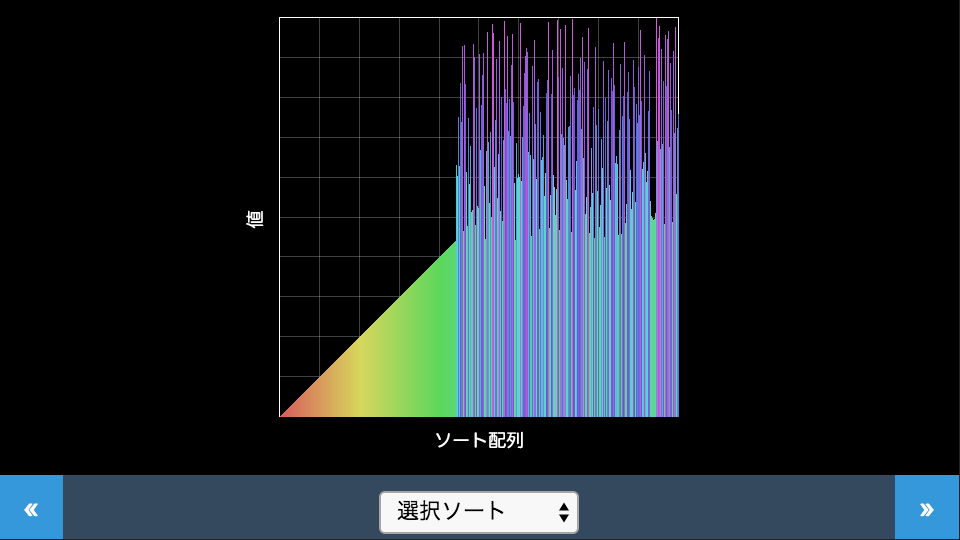
アルゴリズム
データの中から一番小さい値を探し、1番目の要素と交換します。次に2番目以降のデータの中から再度一番小さい値を探し、2番目の要素と交換します。これをデータの最後尾まで繰り返すソートです。デモでは先頭から順番に位置が確定していく様子が見られます。
計算量
比較がnの2重ループになるため、平均計算時間はO(n^2)となります。
オススメ度
★☆☆☆☆(1)
こちらもバブルソートと同じくO(n^2)の比較のため要素数が多くなると遅くなります。ソースコードも単純ですが、データ列によっては早くなる挿入ソートと比べると選択ソートを使う利点はあまりないように思います。選択ソートよりはバブルソートや挿入ソートをオススメします。
ヒープソート
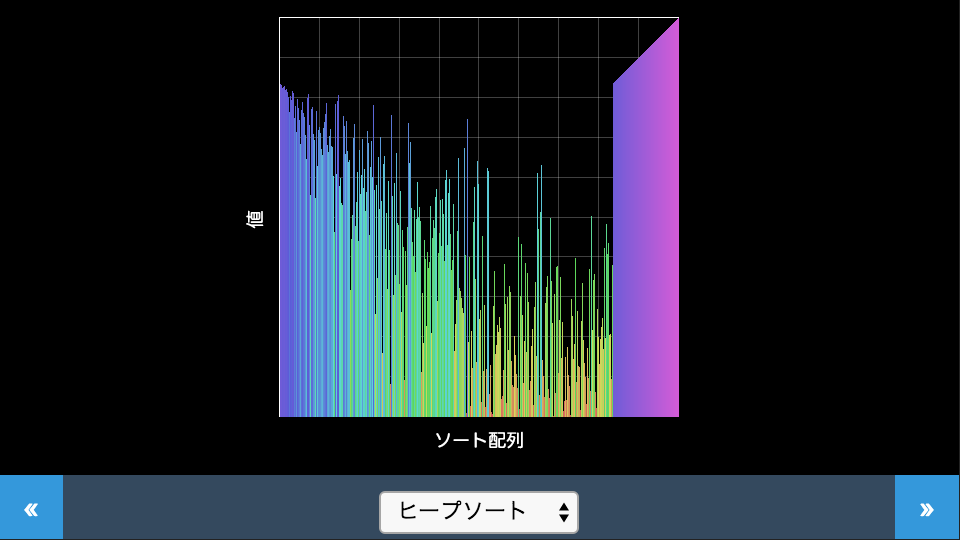
アルゴリズム
データをまず1番目から順に二分ヒープ木と呼ばれる木構造になるように並び替え、その後ヒープから順番に要素を取り出すことで整列します。デモではまず左から二分ヒープ木に追加されていき、その後右から整列されていく様子が見られます。
計算量
平均計算時間はO(nlogn)となります。
オススメ度
★★☆☆☆(2)
一般的に先のバブルソートや選択ソートより高速ですが、プログラムが複雑になるデメリットもあります。また、データ列の状態に対して計算時間のバラつきが少ないため、どんな状態からでも安定した時間でソートができるメリットがあります。
シェルソート

アルゴリズム
挿入ソートの改良系で、データ列を一定間隔で取り出して挿入ソートを行い、間隔を狭めて挿入ソートを繰り返します。挿入ソートは整列に近い状態のデータ列に対しては高速に動作しますが、整列されていないデータ列に対しては低速になります。そこで、あらかじめ挿入ソートが有利なならびになるようおおまかに整列させておくことで処理を高速にする考え方です。デモではデータが平均的になだらかになり、だんだん整列の精度が高くなっていく様子が見られます。
計算量
平均計算時間はO(n^1.25)となります。
オススメ度
★★★★☆(4)
挿入ソートと比べるとプログラムは多少複雑になりますが、挿入ソートのメリットを保ったまま平均的な計算速度を改善したアルゴリズムであり、要素数一万程度のデータ列にオススメです。
マージソート
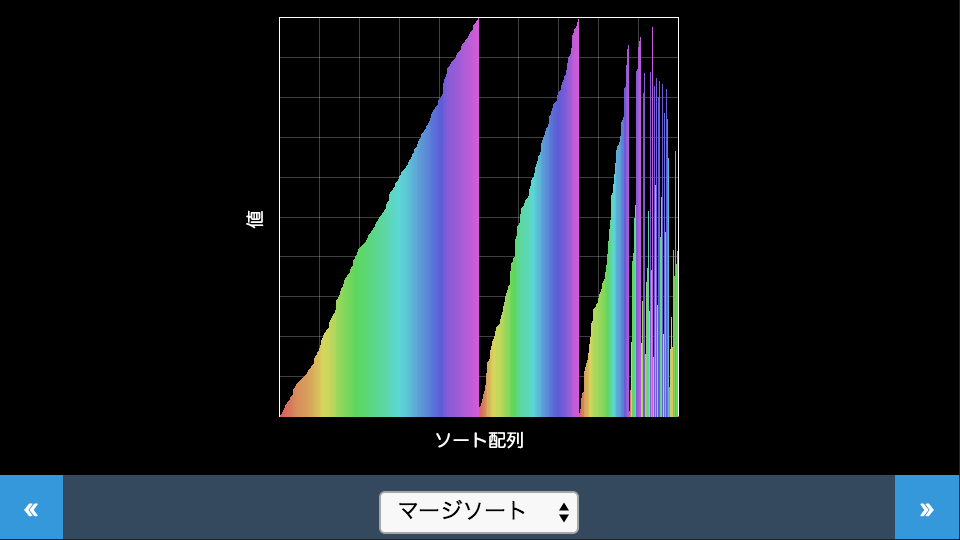
アルゴリズム
まずデータを要素2つずつの組に分解し、その中でそれぞれソートします。その後、ソート済みの2つの組を取り出すと、それぞれの組の先頭を比較していくだけで要素4つの1つの整列済みの組に統合(マージ)できます。同様に8,16…と要素を統合していくことで整列する方法です。デモでは分割されたデータ域がそれぞれ整列されていき、結合していく様子が見られます。
計算量
平均計算時間はO(nlogn)となります。
オススメ度
★★★☆☆(3)
プログラムは複雑になりますが、平均計算時間がO(n^2)となるソートと比べると一般的に高速に動作します。
クイックソート
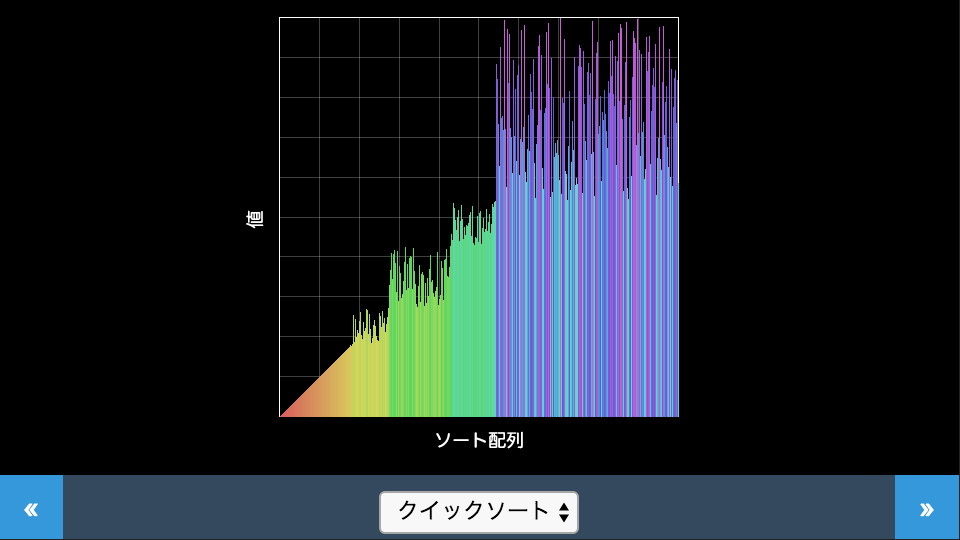
アルゴリズム
データ列の中から適当な数(ピボット)を選択し、左から順番に検索して見つかったピボットより大きな値と右から順番に検索して見つかったピボットより大きな値を入れ替えることで、ピボットより小さい値を前方に、大きな値を後方に移動させます。ピボットに対する位置関係は整列された状態となるため、ピボットの値を変えて同様に整列させていく方法です。デモではピボット付近が部分的になだらかに整列されていく様子が見られます。
計算量
平均計算時間はO(nlogn)となります。
オススメ度
★★★★☆(4)
その名の通り一般的に高速なソートとして知られており、平均計算時間が同じくO(nlogn)となるヒープソートと比べると、多くの場合早い結果となります。プログラムは複雑ですがソート時間を短縮させたい時にオススメです。
おわりに
普段意識していなかったソートアルゴリズムも視覚的に整列されていく様子を見ると、内部でどのような手順になっているか理解が深まると思います。ソートの仕組みがわかるとデータに合わせた最適なアルゴリズムが見えてくるため、HTML5やJavaScriptでのコンテンツ制作時に役立ちます。みなさんも是非用途に合わせたアルゴリズムを選択ください。