プログラムで使うことの多い「乱数」。ゲーム開発やビジュアルアート、ウェブサイトのアニメーションにおいて乱数は非常に重要で、さまざまな用途で利用されています。プログラムで一般に乱数と聞くと、すべての数値が同じ頻度（分布）で出現する「一様乱数」と呼ばれる乱数をイメージする方が多いと思います。

多くの場合はこの「一様乱数」で取得した乱数を用いれば十分でしょう。しかし、場合によっては「一様乱数」ではなく、偏りのある乱数を用いることでコンテンツの見た目や現象の「自然さ」を演出することが可能です。

実は「一様乱数」に一手間加えることで、乱数の分布の偏りを制御できます。今回は乱数を使用して好みの分布を得るためのパターンをいくつか紹介します。

乱数分布のシミュレーションデモ （HTML5製）

次のデモはリアルタイムで乱数の出現頻度を計算し、グラフに可視化するコンテンツです。画面下のプルダウンで乱数の種類を選択すると、選択した方式に応じた乱数の出現頻度分布を表示します。

• デモを別ウインドウで再生する
• ソースコードを確認する

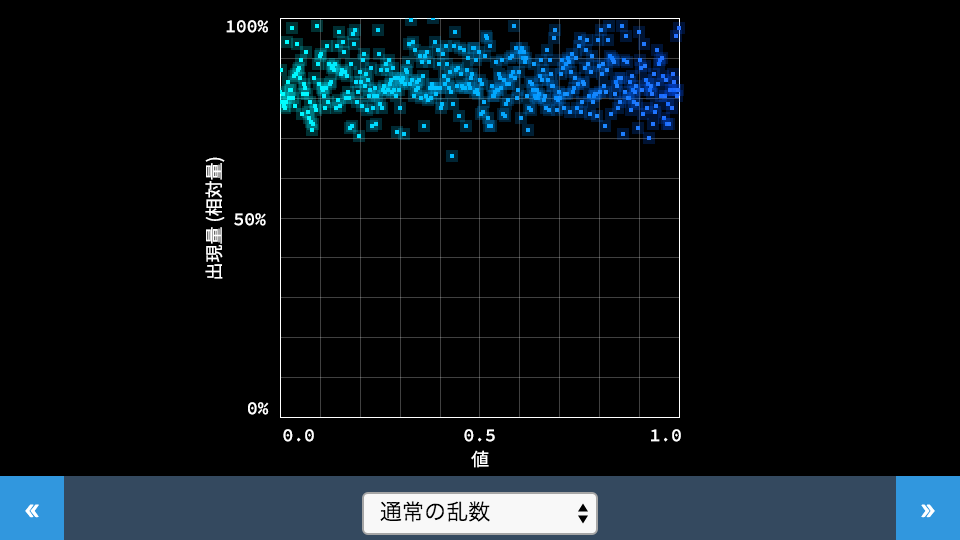
※このデモはCreateJSで開発しています。

それぞれの乱数の数式と傾向・使いどころを紹介します。

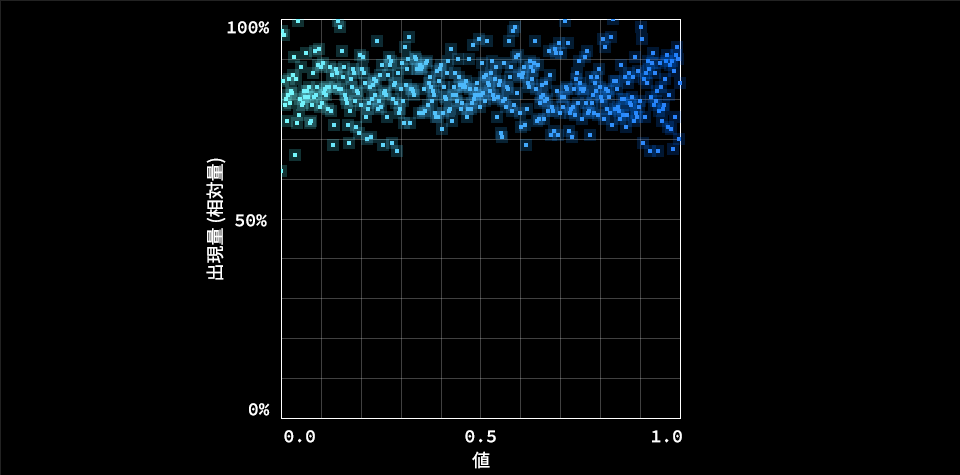
通常の乱数 - 一様乱数

// 通常の乱数
const value = Math.random();

一様乱数と呼ばれ、0.0から1.0までの値が均等に出現する乱数です。JavaScriptなどでMath.random()関数として提供されおり、ほとんどのプログラミング言語で標準で用意されているのはこの一様乱数の関数のみです。普段一番よく使う乱数でしょう。

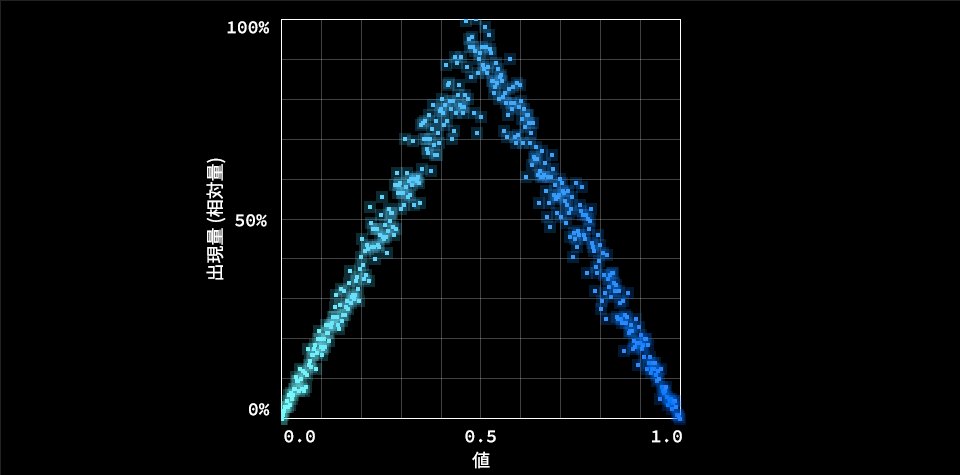
乱数の加算 : 中央に偏らせる

// 乱数の加算
const value = (Math.random() + Math.random()) / 2;

乱数を2回発生させて、足し合わせたものです。分布は直線的になり、中央の値の出現率が高くなります。

乱数の乗算 - ゼロ付近の割合を多くする

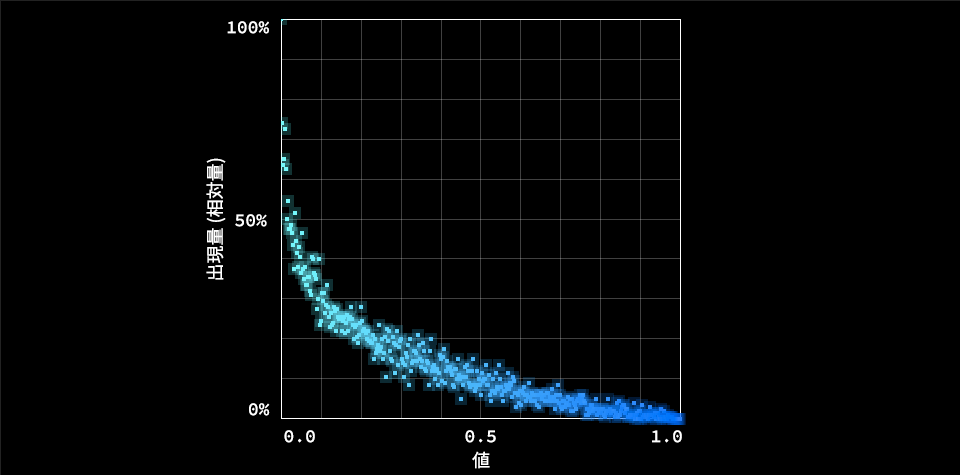
// 乱数の乗算
const value = Math.random() * Math.random();

乱数を2回発生させて、掛け合わせたものです。0.0付近の出現率が高くなります。値が大きくなるにつれて出現率が減るので、自然な偏りをもたせたい場合に使用できます。

乱数の2乗 - ゼロ付近の割合をさらに多くする

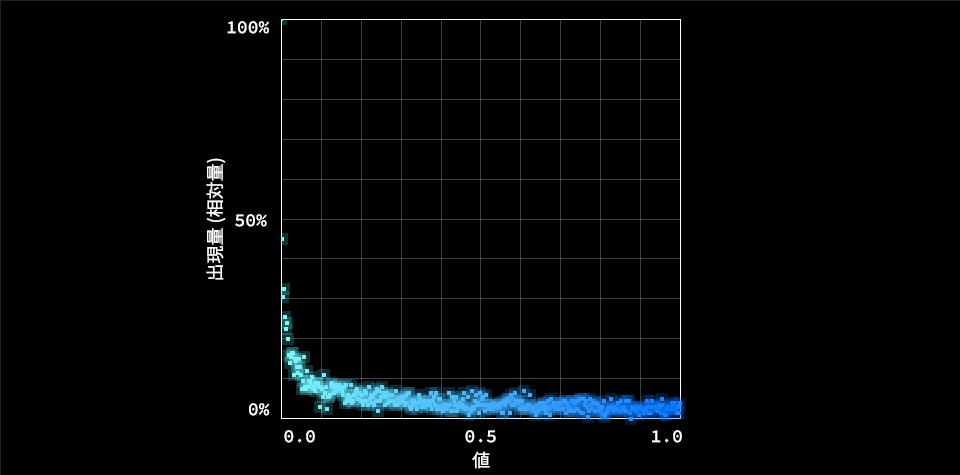
// 乱数の2乗
const r = Math.random();
const value = r * r;

乱数を2乗したもの。0.0付近の出現率が飛び抜けて高くなり、乗算の乱数と比べて急激な分布になります。0.1より高い数値の出現が近くなるのも特徴です。明確に偏りを持たせたい場合はこちらを使用します。このように乱数を組み合わせることでさまざまな分布が得られます。

乱数の平方根

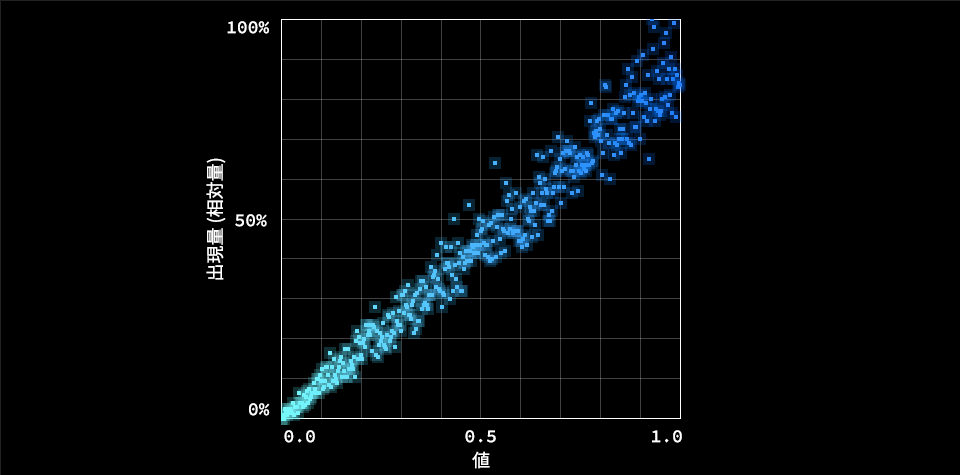
// 乱数の平方根
const value = Math.sqrt(Math.random());

乱数の平方根。出現頻度が0.0から1.0まで直線的に増えていきます。

正規乱数

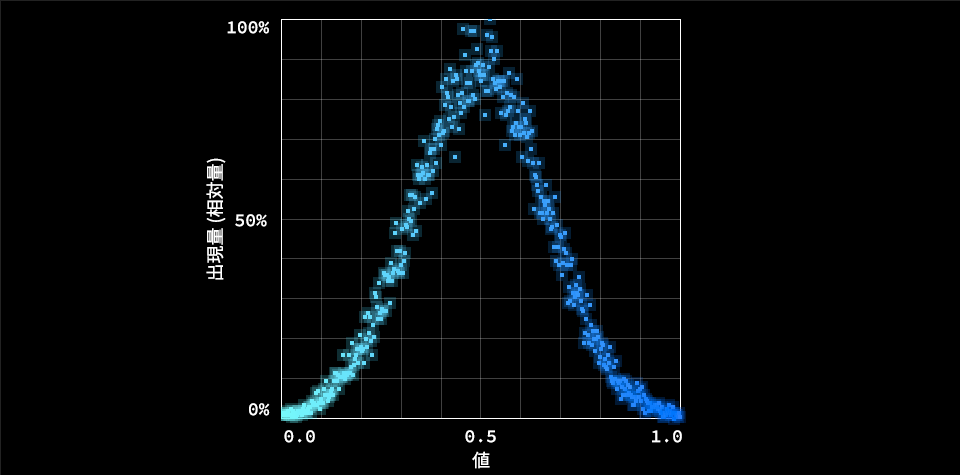
function calcNormal() {
  // 正規乱数
  const r1 = Math.random();
  const r2 = Math.random();
  let value = Math.sqrt(-2.0 * Math.log(r1)) * Math.sin(2.0 * Math.PI * r2);
  // 値を0以上1未満になるよう正規化する
  value = (value + 3) / 6;
  return value;
}

// 0.0未満、1.0以上になるケースがあるため
// その時は再計算を行う
let value;
while (true) {
  value = calcNormal();
  if (0 <= value && value < 1) {
    break;
  }
}
console.log(value);

正規分布と呼ばれる分布の形になる乱数。統計学などでよく使用され、身長や成績など多くの統計的データがこの正規分布に従います。中心部分が一番出現頻度が高く、中心から離れるほど頻度が急激に減少しますが、どんな値でも出現する可能性があります。ごく稀に想定外に飛び抜けた値になることがあるため、実際に使用するときは上限値など範囲を設けて範囲から外れた値は無視します。

分布の反転

// 乱数の乗算
const valueA = Math.random() * Math.random();
// 乱数の反転
const value = 1.0 - valueA;

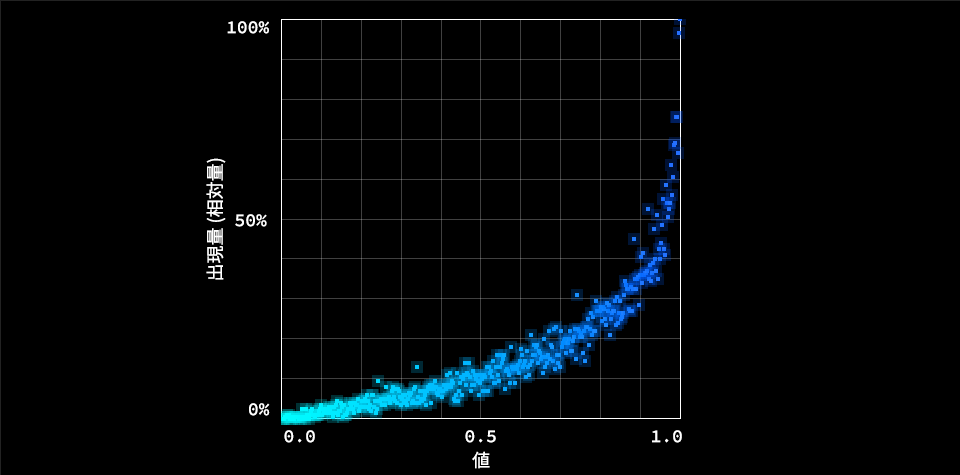
乱数は0.0から1.0までの値となるので、1.0から乱数を引き算することで、反転した分布が得られます。0.0付近の出現頻度が高かった「乱数の乗算」や「乱数の二乗」を反転すると、逆に1.0付近の出現頻度が上がります。

おわりに

分布のある乱数を使い分けることでランダム要素に多様性が加わります。今回紹介した演算方法以外にも、乱数の組み合わせてさまざまな分布の乱数を生成できます。このランダムの発生分布制御は、たとえば当サイトトップページをはじめ、パーティクルのサイズの部分によく利用しています（小さいサイズの発生率を高くしている）。

本記事ではJavaScriptで解説しましたが、他の言語でもロジックは使いまわせます。みなさんも用途に合わせた好みの分布の乱数を使いこなしましょう。